Author:
(1) David S. Hardin, Cedar Rapids, IA USA ([email protected]).
Table of Links
3 The Rust Programming Language
4 RAC: Hardware/Software Co-Assurance at Scale
5.1 Restricted Algorithmic Rust
6 Dancing Links in Rust and 6.1 Definitions
9 Acknowledgments and References
6.3 Dancing Links Theorems
Once we have translated the circular doubly-linked list functions into ACL2, we can begin to prove theorems about the data structure implementation. We begin by defining a “well-formedness” predicate for CDLLs.
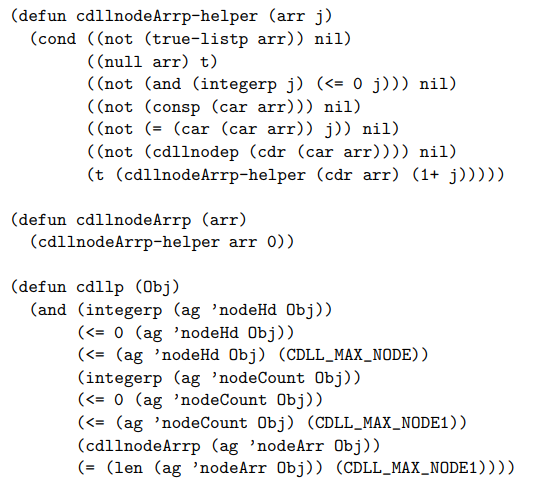
Given this definition of a good CDLL state, we can prove functional correctness theorems for Dancing Links operations, of the sort stated below. Note that this proof requires some detailed well-formedness hypotheses related to the prev and next indices for the nth element:

ACL2 performs the correctness proof for this cdll_restore of cdll_remove theorem automatically. In addition to the Dancing Links operator proofs, we have proved approximately 160 theorems related to the CDLL data structure, including theorems about cdll_cns() (cons equivalent), cdll_- rst() (cdr equivalent), cdll_snc() (add to end of data structure), cdll_tsr() (delete from end of data structure), cdll_nth(), etc. All of these proofs will be made publicly available in the ACL2 workshop books repository.
This paper is available on arxiv under CC BY 4.0 DEED license.